How Is A Clumped Population Distribution Beneficial For Prey Animals?

Density and dispersion are two descriptors of populations that can provide insight into processes such as contest and territoriality. Their measurement is therefore fundamental to our understanding of biogeography.

Populations have several characteristics that ecologists apply to describe them. How individuals are bundled in space, or dispersion, informs united states almost environmental associations and social interactions among individuals in the population. How many organisms there are per unit of measurement area is referred to every bit density. Both of these characteristics tin can exist measured in a variety of ways (Krebs 1999).

Density

Density tin be estimated in a diversity of different ways depending on the organism and habitat you lot are sampling. Quadrat sampling is 1-way ecologists attain this. Quadrat sampling involves deciding what size and shape of surface area you volition sample and deciding how many samples to take. Many studies utilize the literature as a guide to the size and shape of quadrats that tin can be used. It is also plausible to determine what quadrat size and shape are optimal for the study you wish to conduct (Krebs, 1999). This type of method tin be problematic if the organisms you are studying are at low densities and/or occur in clumps across the landscape. Quadrat methods can also be used to extrapolate densities from indirect measures (e.g., brute droppings, tracks, nests).

Although quadrat sampling is simple and widely used, for some organisms it is not appropriate. Thus, many other types of methods have been developed. For many animal populations, mark-recapture methods are utilized where individuals are caught, marked, released and then some other sample taken. The proportion of marked individuals tin can then be used to estimate the full population size. This is chosen the Peterson method and is the simplest of the many mark-recapture methods available to ecologists (Krebs 1999). For animals or plants that are sedentary or tin be identified and located before they move, plotless methods, like the line-intercept method, can be practical (Krebs 1999).

The density of organisms varies depending on a variety of factors. Deaths, births, immigration, and emigration are all processes that tin can impact population density at a given time. Nevertheless, there are general trends associated with density. For instance, across a number of species, smaller organisms tend to occur at higher densities than larger organisms (White et al. 2007, Lewis et al. 2008, Rossberg et al. 2008). Although our understanding of these processes and patterns associated with density has improved, there is still an enormous amount of descriptive and experimental work needed to understand how organismal characteristics are associated with density (Blackburn et al. 2006).

Dispersion

Patterns of Dispersion

How individuals are arranged in space tin tell you a great bargain about their ecology. For instance, Figure 1 shows the distribution of a hypothetical species. Well-nigh people would describe this every bit a random pattern in space. However, if you lot look closely yous will notice that individuals are non actually randomly distributed, they are maintaining a fairly uniform altitude between each other. Why exercise you think that is? Figure two shows the distribution of another hypothetical species. This fourth dimension they are grouped together in certain v x v meter areas just not in others. What might this tell you about this species and its interactions with the environment? Figure 3 shows the distribution of individuals of a hypothetical species that is actually random. One affair that y'all'll notice is that it is difficult to think of this as random!

Figure i: Clumped dispersion of individuals

The boilerplate number of individuals per square is vi.25, the variance is 125, and the ratio of the two is twenty.

These iii figures illustrate the three different patterns of dispersion that ecologists observe. Clumped dispersion (Figure one) where individuals are aggregated in certain areas of the sampled space. Compatible dispersion (Figure 2), where individuals are almost equally spaced apart from each other and random dispersion (Figure 3).

Figure 2: Compatible dispersion of individuals

The average number of individuals per square is 10, and the variance is 4.27. The variance to mean ratio is 0.427.

Behavioral and ecological factors influence dispersion. Uniform patterns of dispersion are generally a issue of interactions between individuals like competition and territoriality. Clumped patterns usually occur when resource are concentrated in small areas within a larger habitat or considering of individuals forming social groups. At large spatial scales about organisms appear to have clumped distributions because their habitats are not uniformly distributed over broad areas. Although you might not call up of plants equally territorial, they likewise can have compatible dispersion patterns that are a result of territoriality and competition (eastward.g., shading, allelopathy, and root interactions; Mahall & Callaway 1992, Schenk et al. 1999). Random dispersion patterns are singular in nature and could indicate a uniform or random distribution of resources or a lack of interactions amid individuals in the population.

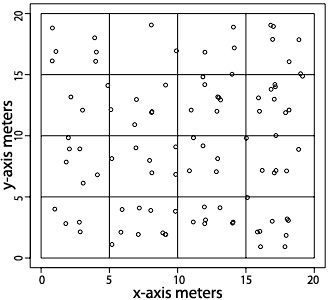
Figure three: Random dispersion of individuals

The mean number of individuals per square is 5.94, the variance is five, and the ratio is 0.841.

Which Dispersion Pattern is it?

Humans are not ever very good at distinguishing amidst the different patterns of dispersion, so statistical methods are ordinarily used to tell the difference between them.

A very simple method that can be used to decide dispersion patterns is based on the sample mean and variance of the number of individuals counted in repeated quadrats in a particular area that is sampled. The sample mean is the average collected from the sample. As an example, let'southward examine Effigy 1. This figure is divided into squares, and each square represents a sample of organisms in infinite. In this case the organisms are clumped in space and there are four samples with 25 organisms and 12 with no organisms. The sample hateful is calculated every bit the sum of all of the observations (25 + 25 + 25 + 25 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0) divided past the full number of samples (16). Thus the mean number per square in Effigy 1 is 6.25. The variance is calculated by squaring the differences between the sample mean and each of the observations, calculation them up to produce the sum of the squares, and dividing past the sample size minus ane. So the variance in this instance would be ([25 - 6.25]² + [25 - 6.25]² + [25 - 6.25]² + [25-half-dozen.25]ⁱⁱ + [0 - half dozen.25]^two + [0 - 6.25]² + [0 - half dozen.25]² + [0 - 6.25]² + [0 - 6.25]² + [0 - 6.25]² + [0-6.25]² + [0 - half-dozen.25]² + [0 - 6.25]² + [0 - half dozen.25]² + [0 - 6.25]^two)/(sixteen - 1) which is 125. And so in Figure ane the average number of individuals per grid foursquare is half-dozen.25 and the variance among grid squares is 125. The ratio of the variance to the mean can then be used to decide whether the pattern is uniform or clumped, and is referred to as the alphabetize of dispersion (Krebs 1999). In this case the ratio is twenty, which is much greater than one! This indicates that individuals in this population are exhibiting a clumped spacing pattern in the sampled habitat. If this ratio is less than one, it indicates a uniform distribution (eastward.g., Figure 2, ratio = 0.427). Whereas if it is one, that indicates individuals are randomly distributed in space (e.g., Figure 3, ratio = 0.841). While this method is extraordinarily simple and widely illustrated in many texts, information technology can potentially fail to observe some not-random patterns of dispersion (see Krebs 1999).

The distances between individuals tin can also be used to determine dispersion patterns. Several indices exist, but all operate using like principles. If individuals are aggregated or clumped (Figure 2), their nearest neighbor will be much closer than yous would wait if individuals were randomly distributed in infinite (Effigy 3). If they were uniformly distributed (Figure 1), on boilerplate, you lot would predict individuals to exist farther apart than would be expected if they were randomly distributed.

A Example Study: Dispersion Patterns in Spiders

Figure 4:Agelenopsis sp. on a sail web

© Creative Commons Patrick0Moran via Wikimedia Commons Some rights reserved.

Agelenopsis aperta is a canvass-web weaving spider found in the grasslands of the desert southwest (Riechert & Gillespie 1986). These spiders build sheet webs that resemble funnels and are in the family unit Agelenidae (Effigy 4). At a modest scale (i–3 m) spiders are uniformly distributed. All the same, at a larger scale the spiders are clumped. Why?

Explaining these patterns requires investigation of the availability of suitable habitat as well as the interactions among individuals. At a larger spatial scale a very small-scale amount of the habitat is suitable for websites and, of course, that is where the spiders are (Riechert 1981). These spiders prefer large depressions in grassland habitats with characteristics bonny to insect prey (eastward.g., flowering shrubs, the presence of litter, and animal feces) and have favorable thermal properties (Reichert & Gillespie 1986). The spatial distribution of these suitable habitats is what generates the clumped pattern at a larger scale. Since high quality websites are limited in the habitat, and the presence of other spiders in close proximity reduces the fitness of the resident spider, residents will actively patrol their website and appoint in aggressive behavior towards other spiders enter into their territory (Riechert 1981). These interactions generate a minimum spacing among individuals inside suitable habitat patches, and the occasional displacement of individuals from their website (Riechert 1981, Riechert & Gillespie 1986). Aggressive interactions like these are typical of the types of behavioral interactions that generate uniform spacing patterns.

References and Recommended Reading

---

Blackburn, T. M., Cassey, P., & Gaston, Yard. J. Variations on a theme: Sources of heterogeneity in the interspecific human relationship between abundance and distribution. Journal of Animal Ecology 75, 1426–1439 (2006).

Krebs, C. J. Ecological Methodology, second ed. Menlo Park, CA: Longman, 1999.

Lewis, H. M., Law, R., & McKane, A. J. Affluence-trunk size relationships: the roles of metabolism and population dynamics. Journal of Animal Ecology 77, 1056–1062 (2008).

Mahall, B. E., & Callaway, R. Grand. Root advice: Mechanisms and intracommunity distributions of two Mojave desert shrubs. Ecology 73, 2145–2151 (1992).

Riechert, S. E. The consequences of being territorial: Spiders, a instance study. American Naturalist 117, 871–892 (1981).

Riechert, S. E., & Gillespie, R. G. "Habitat option and utilization in web building spiders." In Spiders: Webs, Behavior, and Evolution, ed. W. A. Shear (Palo Alto, CA: Stanford University Printing, 1986): 23–28.

Rossberg, A. G. et al. The peak-downward mechanism for body-mass-abundance scaling. Environmental 89, 567–580 (2008).

Schenk, H. J., Callaway, R. Chiliad., & Mahall, B. Due east. Spatial root segregation: Are plants territorial? Advances in Ecological Research 28, 145–180 (1999).

White, E. P. et al. Relationships between body size and abundance in ecology. Trends in Ecology and Evolution 22, 323–330 (2007).

Source: https://www.nature.com/scitable/knowledge/library/density-and-dispersion-19688035/

Posted by: hinesthessfy63.blogspot.com

Share this post